| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- bitmasking
- gradlew
- 15829
- PYTHON
- CSS
- flexbox
- BOJ
- JAVA14
- WRAP
- margin-collapsing
- 자료구조
- Range
- Flex
- 백준
- FlexItem
- HTML
- MariaDB
- MacOS
- 9935
- db
- C
- dp
- JAVA11
- 2098
- MAC
- springboot
- gradle
- spring
- 마진 상쇄
- heroku
개인기록
[C/Python] 백준 2098 외판원 순회 본문
https://www.acmicpc.net/problem/2098
2098번: 외판원 순회
첫째 줄에 도시의 수 N이 주어진다. (2 ≤ N ≤ 16) 다음 N개의 줄에는 비용 행렬이 주어진다. 각 행렬의 성분은 1,000,000 이하의 양의 정수이며, 갈 수 없는 경우는 0이 주어진다. W[i][j]는 도시 i에서 j
www.acmicpc.net
이 문제의 키워드는 다음과 같이 정리할 수 있다
" 어느 한 도시에서 출발해 N개의 도시를 모두 거쳐 다시 원래의 도시로 돌아오는 순회 경로 "
" 한 번 갔던 도시로는 다시 갈 수 없다 "
" 도시의 수 N ~ (2 ≤ N ≤ 16) "
순회 경로를 찾고 있으므로 시작점이 어디인지는 중요하지 않다.
그러니까 편의상 출발은 항상 1번 도시에서 하는 걸로 생각하기로 하자.
이제 가장 적은 비용이 드는 순회 경로를 찾으려면 주어진 입력에서 가능한 경로를 모두 탐색하면서
한 번 방문한 도시는 다시 방문하지 않도록 각 탐색마다 이전에 방문했던 도시들을 각각 기록해야 한다.
예를 들자면 현재 2번 도시(기존 1번 도시 방문), 현재 3번 도시(기존 1번, 2번, 5번 도시 방문), ...
이런 식의 상태 저장이 필요하다는 얘기다.
주어진 입력에서 가능한 탐색을 모두 수행하고 있으므로
같은 3번 도시에 도착했더라도 1번->2번->3번 도시 경로일 수도 있고, 1번->4번->2번->3번 도시 경로일 수도 있다.
다행히 이 문제에서는 2 ≤ N ≤ 16 으로 N에 매우 작은 수라는 제한이 걸려있기 때문에 비트마스킹 기법을 사용할 수 있다.
즉, 아직 방문하지 않은 도시라면 0, 이미 방문한 도시라면 1로 표현함으로써 방문 여부를 체크하는 방식이다.
이 문제에서는 1번부터 N번까지의 도시가 주어지므로 각 도시의 번호를 비트의 인덱스로 사용하면 된다.
(코드의 편의성을 위해 앞으로 도시의 번호는 0번부터 시작하는 것으로 생각하자. 1번부터 N번 도시를 0번부터 N-1번 도시로 치자는 소리다.)
글로만 쓰면 이해가 어려우므로 백준에 주어진 예제를 통해 알아보자.
예제에서와 같이 4개의 마을이 있는 경우, dp 테이블은 다음과 같이 (도시의 개수)x(각 도시 방문 여부)의 크기로 만들 수 있다.
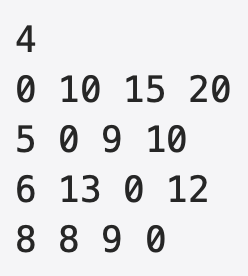

위의 예시에서 0번->1번->3번 도시 순으로 방문했다면 현재 상황은 dp[3][1011](실제로는 dp[3][11]) 로 나타낼 수 있다.
0번->2번 도시 순으로 방문했다면 현재 상황은 dp[2][0101](실제로는 dp[2][5]) 로 나타낼 수 있다.
이처럼 모든 상황의 Yes/No의 판단이 필요한 경우 비트를 사용하면 다른 방법보다 훨씬 간결하게, 그리고 빠르게 나타낼 수 있다.
외판원 순회 문제에서의 점화식은 아래와 같이 나타낼 수 있다.
(now는 현재 도시, visited는 위에서 설명한 비트마스킹 방법으로 나타낸 도시 방문 여부(e.g. 0011)이다.)
TSP(now, visited) =
if visited == U, then return W(now, 0)
else return min( TSP(v, visited ∪ {v}) + W(now, v), where v is not visited)
만약 현재 도시가 순회할 마지막 도시라면 현재 마을에서 시작점인 0번 도시까지의 거리를 반환하고,
만약 더 방문해야 할 도시가 있다면 현재 도시에서 다음으로 방문 가능한 도시들에 대해 TSP 함수를 재귀 호출하여
해당 도시에서의 반환값과 현재 도시에서 해당 도시까지의 거리를 더한 값이 가장 작은 것을 반환한다.
위 점화식의 else 부분을 위의 예시를 이용해 같이 살펴보도록 하자.
우리는 편의상 항상 0번 도시에서 출발하기로 했으므로 처음의 visited는 0번 도시만 방문했음을 뜻하는 0001일 것이다.
따라서 TSP 함수의 첫 호출 인자는 0(now)과 1(visited)이 된다.
0번 도시에서 방문 가능한 도시는 1번 도시, 2번 도시, 3번 도시가 있다.
각각에 대해 도시 번호와 갱신된 visited를 인자로 하여 TSP 함수를 호출하는 식으로 계속 진행하면 다음과 같을 것이다.

모든 도시를 방문할 때까지 계속해서 재귀 호출되는 TSP 함수는 마지막 도시, 즉 비트가 전부 1인 경우 점화식의 if 부분대로 해당 도시에서 0번 도시로 돌아가는 비용을 반환하게 된다.
그 전까지 거치는 중간 도시에서의 각 TSP 함수는 위와 같은 과정을 통해 해당 도시 이후로 가능한 경로 중 최소값을 dp 테이블에 저장하게 된다.
예를 들어 TSP(3, 9)의 경우 0번 도시, 3번 도시를 방문한 이후로 갈 수 있는 경로 중 최소값을 dp[3][9]에 저장하게 되고,
TSP(1, 7)의 경우 0번, 2번, 1번 도시를 방문한 이후로 갈 수 있는 경로 중 최소값을 dp[1][7]에 저장하게 되는 것이다.
결과적으로 모든 함수 호출이 끝난 뒤에는 dp[0][1]에 0번 도시를 시작점으로 하여 갈 수 있는 경로 중 최소 비용의 값이 저장된다.
+ 비트마스킹 문제에서 주로 사용되는 비트 연산 기능 정리
1. Reset
1111 & ~(1 << 2) => 1111 & 1011 = 1011
: 2 자리에 들어가는 인덱스의 비트를 0으로 만든다
2. Set
0000 | 1 << 2 => 0000 & 0100 = 0100
: 2 자리에 들어가는 인덱스의 비트를 1로 만든다
3. Toggle
1111 ^ (1 << 2) => 1111 ^ 0100 = 1011
: 2 자리에 들어가는 인덱스의 비트를 반전시킨다
4. Check
1010 & (1 << 2) => 1010 & 0100 = 0
1110 & (1 << 2) => 1110 & 0100 = 100
: 2 자리에 들어가는 인덱스의 비트 값이 0이라면 결과값이 0이 나온다 => 해당 비트가 0인지 1인지 판단 가능
[C 코드]
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define INF 100000000
#define MAX 16
#define min(a, b) a<b? a : b
int N;
int dp[MAX][1 << MAX];
int w[MAX][MAX];
int tsp(int now, int visited) {
if (visited == (1 << N) - 1) { // 모든 도시를 다 방문한 경우
if (w[now][0] != 0) // 0번 도시(시작점)로 돌아가서 종료
return w[now][0];
else return INF; // 0번 도시로 돌아갈 수 없는 경우 INF 반환
}
if (dp[now][visited] != -1) // 이미 방문한 도시인 경우
return dp[now][visited];
else dp[now][visited] = INF;
for (int next = 0; next < N; next++) { // 다음으로 방문할 도시 찾기
if ((visited & (1 << next)) || w[now][next] == 0)
continue; // 방문했거나 갈 수 없는 도시는 제외
dp[now][visited] = min(dp[now][visited],
tsp(next, visited | (1 << next)) + w[now][next]);
// 시작점까지의 순회 경로가 가장 짧은 도시를 다음 도시로 선택
}
return dp[now][visited];
}
int main() {
scanf("%d", &N);
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
scanf("%d", &w[i][j]);
memset(dp, -1, sizeof(dp));
printf("%d\n", tsp(0, 1));
}
[Python 코드]
INF = 1000000000
def tsp(now, visited):
if visited == (1 << N) - 1: # 모든 도시를 다 방문한 경우
if w[now][0] != 0: # 0번 도시(시작점)로 돌아가서 종료
return w[now][0]
else: return INF # 0번 도시로 돌아갈 수 없는 경우 INF 반환
if dp[now][visited] != 0: # 이미 방문한 도시인 경우
return dp[now][visited]
else: dp[now][visited] = INF
for next in range(N): # 다음으로 방문할 도시 찾기
if ((visited & (1 << next)) or w[now][next] == 0):
continue # 방문했거나 갈 수 없는 도시는 제외
dp[now][visited] = min([dp[now][visited],
tsp(next, visited | (1 << next)) + w[now][next]]);
# 시작점까지의 순회 경로가 가장 짧은 도시를 다음 도시로 선택
return dp[now][visited];
N = int(input())
w = []
for _ in range(N):
li = list(map(int, input().split()))
w.append(li)
dp = [[0]*(1 << N) for _ in range(N)]
print(tsp(0, 1))

